ممان اینرسی سطح و مفاهیم مربوط به آن

ممان اینرسی سطح که گشتاور دوم سطح نیز نامیده می‌شود، پارامتری است که تعیین می‌کند یک شکل (مانند سطح مقطع تیر)، به دلیل هندسه‌اش، چه مقدار در برابر خمیدگی مقاومت دارد.

تخته نازکی را در نظر بگیرید که بار 100 کیلوگرمی را تحمل میکند. هنگامی که بار را روی تختهای که بهصورت افقی قرار داده شده میگذاریم، مقاومت کمتری نسبت به خمش دارد. این موضوع به این دلیل است که مقاومت در برابر خمش به نحوه توزیع مصالح روی سطح مقطع نسبت به محور خمشی بستگی دارد. تخته سمت چپ دارای مصالح بیشتری نسبت به محور خمش است که باعث مقاومت بیشتر میشود.

این مقاومت در برابر خمش را میتوان با محاسبه ممان اینرسی سطح تعیین کرد. ممان اینرسی سطح با حرف I نشان داده میشود، واحد آن طول به توان چهارم است که به طور معمول برحسب mm یا in می باشد. این پارامتر نشان دهنده نحوه ی توزیع مصالح روی سطح مقطع نسبت به یک محور خاص است. این ویژگی منحصر به فرد یک سطح مقطع نیست، بسته به محور خمشی که در نظر گرفته میشود متفاوت است.

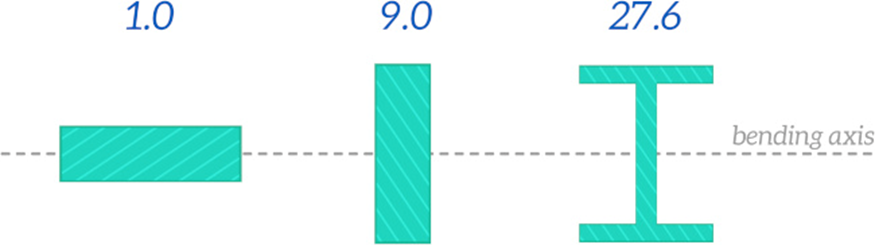
بیایید مقادیر ممان را که برای چند سطح مقطع مختلف محاسبه شده، برای محور خمشی که در زیر نشان داده شده است مقایسه کنیم.
سطح مقطعی که قسمت زیادی از مصالح را دور از محور خمشی قرار میدهند، گشتاورهای اینرسی بیشتری دارند و خم کردن آنها دشوارتر است. این یکی از دلایلی است که I-beam یک سطح مقطع متداول برای کاربردهای سازهای است. بیشتر مصالح در فاصله ی دوری از محور خمشی قرار دارند که باعث می‌شود در برابر خم شدن بسیار کارآمد باشد، در حالی که از مقدار کمی ماده استفاده می‌کند.

مفاهیم اساسی ممان اینرسی سطح

ممان اینرسی سطح به دو بخش اصلی تقسیم می‌شود:

ممان اینرسی سطح اول: که بیانگر توزیع سطح نسبت به یک محور است.
ممان اینرسی سطح دوم: که بیشتر در مهندسی سازه و مکانیک کاربرد دارد و معیاری برای مقاومت سطح در برابر خمش است.

کاربردهای ممان اینرسی سطح

ممان اینرسی سطح در طراحی و تحلیل سازه‌ها، تیرها، ستون‌ها، و دیگر قطعات مکانیکی به کار می‌رود. این مفهوم به مهندسان کمک می‌کند تا بتوانند سازه‌های مقاوم و پایدار طراحی کنند که در برابر نیروهای مختلف مقاومت کنند.

نحوه محاسبه ممان اینرسی سطح

برای محاسبه ممان اینرسی سطح، از فرمول‌های مختلفی استفاده می‌شود که بستگی به شکل و توزیع سطح دارد. برخی از این فرمول‌ها عبارتند از:

ممان اینرسی مستطیل: $\frac{1}{12} b h^3$
ممان اینرسی دایره: $\frac{\pi}{64} d^4$

تفاوت ممان اینرسی سطح و ممان اینرسی جرم

ممان اینرسی جرم مربوط به توزیع جرم جسم نسبت به یک محور چرخش است، در حالی که ممان اینرسی سطح به توزیع سطح جسم نسبت به یک محور اشاره دارد. هر دو مفهوم در تحلیل‌های مختلف مکانیکی و سازه‌ای اهمیت دارند اما کاربردهای متفاوتی دارند.

استانداردها و واحدهای اندازه‌گیری

ممان اینرسی سطح معمولاً با واحدهای میلی‌متر به توان چهارم ( $mm^4$ ) یا متر به توان چهارم ( $m^4$ ) اندازه‌گیری می‌شود. استانداردهای مختلفی برای محاسبه و استفاده از ممان اینرسی وجود دارد که در مهندسی به کار می‌روند.

تأثیر شکل و ابعاد بر ممان اینرسی سطح

شکل و ابعاد سطح تأثیر زیادی بر ممان اینرسی آن دارند. به عنوان مثال، یک تیر با مقطع مستطیلی با ابعاد بزرگتر، ممان اینرسی بیشتری نسبت به یک تیر با مقطع کوچکتر دارد. همچنین، شکل مقطع نیز می‌تواند بر ممان اینرسی تأثیر بگذارد.

ممان اینرسی مقاطع مرکب

در بسیاری از موارد، مقاطع مرکب از ترکیب چندین مقطع ساده تشکیل می‌شوند. برای محاسبه ممان اینرسی این مقاطع، می‌توان از اصل جمع‌پذیری استفاده کرد و ممان اینرسی هر بخش را به طور جداگانه محاسبه و سپس با هم جمع کرد.

مثال‌های عملی از محاسبه ممان اینرسی سطح

برای درک بهتر ممان اینرسی سطح، چند مثال عملی از محاسبه آن ارائه می‌دهیم:

مثال 1: ممان اینرسی یک تیر مستطیلی فرض کنید یک تیر با مقطع مستطیلی به ابعاد $b = 10$ سانتی‌متر و $h = 20$ سانتی‌متر داریم. ممان اینرسی سطح این تیر برابر است با: $\frac{1}{12} b h^3 = \frac{1}{12} \times 10 \times (20)^3 = 13333.33 \, mm^4$

مثال 2: ممان اینرسی یک دایره فرض کنید یک دایره به قطر $d = 5$ سانتی‌متر داریم. ممان اینرسی سطح این دایره برابر است با: $\frac{\pi}{64} d^4 = \frac{\pi}{64} \times (5)^4 = 30.68 \, mm^4$

ممان اینرسی در سازه‌های مهندسی

ممان اینرسی سطح در طراحی و تحلیل سازه‌های مختلف از جمله پل‌ها، ساختمان‌ها و ماشین‌آلات نقش بسیار مهمی دارد. مهندسان با استفاده از این مفهوم می‌توانند سازه‌هایی طراحی کنند که در برابر نیروهای مختلف از جمله بارهای زنده و مرده، باد، زلزله و دیگر نیروها مقاومت کنند.

نرم‌افزارهای محاسبه ممان اینرسی

برای محاسبه ممان اینرسی سطح، نرم‌افزارهای مختلفی وجود دارد که می‌توانند به مهندسان در تحلیل و طراحی سازه‌ها کمک کنند. برخی از این نرم‌افزارها شامل ANSYS، SolidWorks، AutoCAD و SAP2000 هستند که ابزارهای قدرتمندی برای محاسبه و تحلیل ممان اینرسی ارائه می‌دهند.

نتیجه‌گیری

ممان اینرسی سطح یکی از مفاهیم اساسی در مهندسی مکانیک و سازه است که نقش مهمی در تحلیل و طراحی سازه‌ها ایفا می‌کند. با شناخت دقیق این مفهوم و استفاده از آن در طراحی سازه‌ها، می‌توان سازه‌هایی مقاوم و پایدار ایجاد کرد که در برابر نیروهای مختلف مقاومت کنند.

پرسش‌های متداول

1. ممان اینرسی سطح چیست؟ ممان اینرسی سطح معیاری است که مقاومت یک سطح در برابر تغییر شکل یا خمش را سنجش می‌کند و بیشتر در مهندسی سازه و مکانیک مورد استفاده قرار می‌گیرد.

2. تفاوت بین ممان اینرسی سطح و ممان اینرسی جرم چیست؟ ممان اینرسی جرم مربوط به توزیع جرم جسم نسبت به یک محور چرخش است، در حالی که ممان اینرسی سطح به توزیع سطح جسم نسبت به یک محور اشاره دارد.

3. چگونه می‌توان ممان اینرسی سطح را محاسبه کرد؟ ممان اینرسی سطح با استفاده از فرمول‌های مختلفی که بستگی به شکل و توزیع سطح دارد، محاسبه می‌شود. به عنوان مثال، ممان اینرسی یک تیر مستطیلی برابر است با $112bh3\frac{1}{12} b h^3$ .

4. چه عواملی بر ممان اینرسی سطح تأثیر می‌گذارند؟ شکل و ابعاد سطح تأثیر زیادی بر ممان اینرسی آن دارند. شکل مقطع و اندازه‌های سطح از عوامل اصلی تأثیرگذار بر ممان اینرسی هستند.

5. ممان اینرسی سطح در چه صنایعی کاربرد دارد؟ ممان اینرسی سطح در طراحی و تحلیل سازه‌ها، تیرها، ستون‌ها، و دیگر قطعات مکانیکی کاربرد دارد و به مهندسان کمک می‌کند تا سازه‌های مقاوم و پایدار طراحی کنند.

پیشنهاد مکتبی نو: مخازن تحت فشار

آموزش شیت متال در سالیدورک

آموزش موشن استادی در سالیدورک

ممان اینرسی سطح در مقابل گشتاور دوم سطح

هر دو اصطلاح “گشتاور دوم سطح” و “ممان اینرسی سطح” به طور متناوب مورد استفاده قرار میگیرند. با این وجود، برای جلوگیری از هرگونه ابهام با ممان اینرسی سطح، که پارامتری کاملاً متفاوت است و مقاومت یک جسم در برابر شتاب زاویهای را توصیف میکند، اغلب استفاده از اصطلاح “گشتاور دوم سطح” ترجیح داده میشود. اگرچه محاسبه ممان اینرسی سطح و گشتاور دوم سطح از نظر ریاضی شبیه به هم است، اما پارامترهای کاملاً متفاوتی هستند. ممان اینرسی به طور معمول برای توصیف مقاومت یک جسم در برابر چرخش در اطراف محور خود استفاده میشود، در حالی که گشتاور دوم سطح، برای توصیف مقاومت یک شکل در برابر خم شدن استفاده میشود.

نحوه ی محاسبه ی ممان اینرسی سطح

برای هر سطح مقطع دلخواهی مانند سطح مقطع نشان داده شده در تصویر زیر، ممان اینرسی سطح یا گشتاور دوم سطح را میتوان با استفاده از این معادله محاسبه کرد:

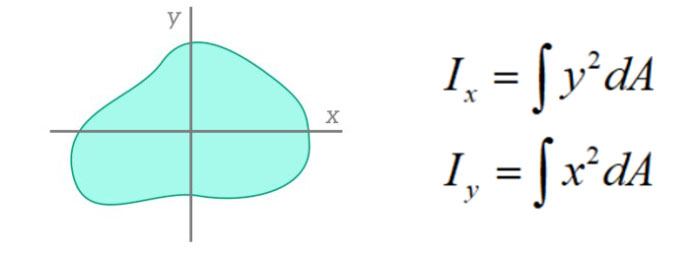
عبارت‌های “x” و “y” نشان می‌دهند که ممان اینرسی سطح به ترتیب برای خمش حول محور و محور محاسبه می‌شود.

بیایید یک مثال ببینیم که چگونه می‌توان از این معادله برای محاسبه ممان اینرسی سطح، یک سطح مقطع مستطیلی استفاده کرد.

مثال – سطح مقطع مستطیلی

ما از معادله نشان داده شده در بالا برای محاسبه ممان اینرسی سطح حول محور x برای سطح مقطع عرضی زیر استفاده خواهیم کرد.

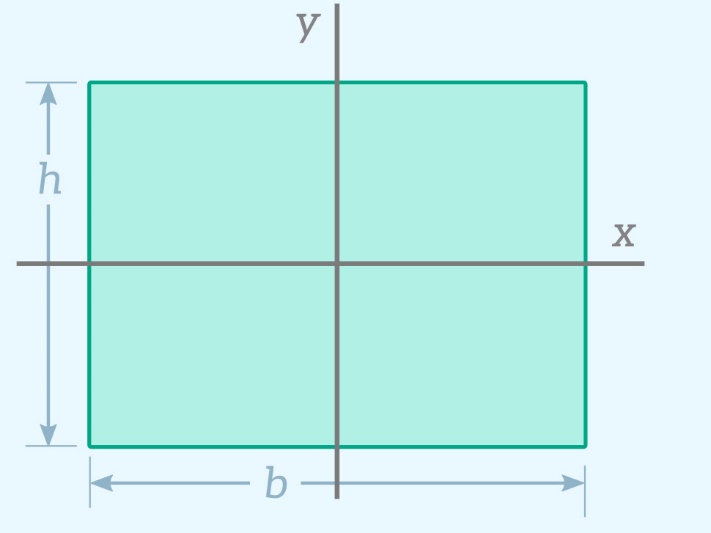
ما می‌توانیم این سطح مقطع مستطیلی را به عنوان مجموعه ای از نوارهای بسیار نازک با عرض b و ارتفاع dy در نظر بگیریم.

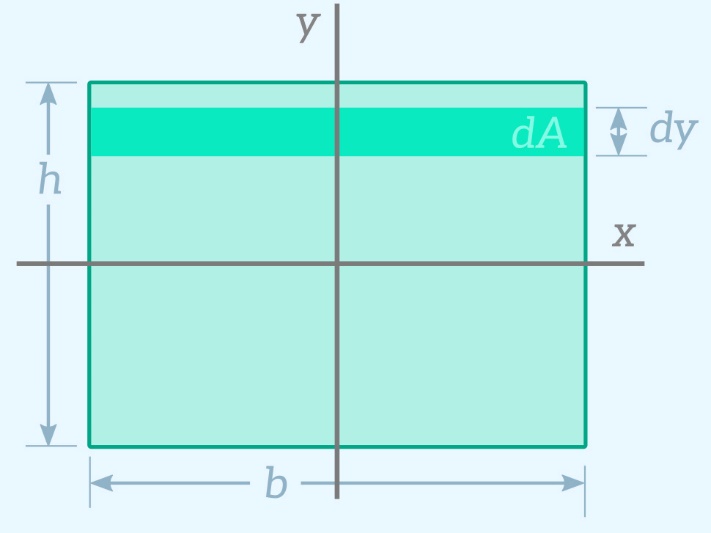
هر نوار به ممان اینرسی سطح کمک میکند. به همین دلیل است که ما برای محاسبه اثر این نوارهای بسیار کوچک انتگرال می‌گیریم.

از آنجایی که عبارت y به توان دو رسیده است، نوارهای در فاصله ی دورتر از محور خمشی (محور x) بسیار بیشتر از نوارهای نزدیک به محور I کمک کننده است.

برای محاسبه فقط کافیست از پایین مستطیل تا بالای مستطیل انتگرال بگیریم.

I=bh3/12

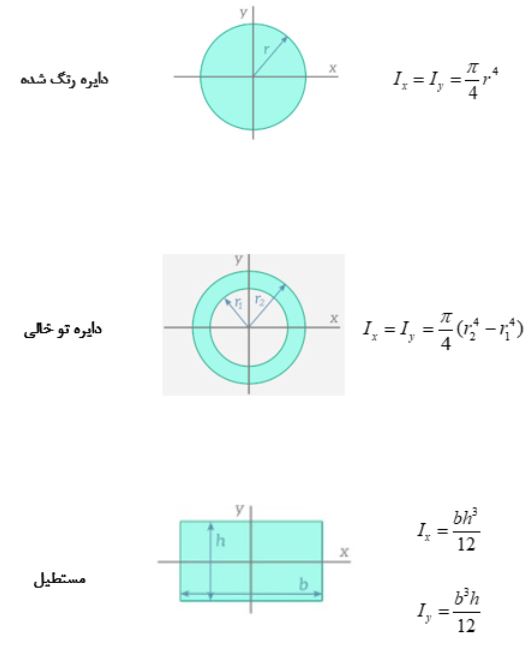
خوشبختانه، هر زمان که نیاز به محاسبه برای یک سطح مقطع عرضی و محور خمشی داشته باشید، نیازی به انجام این فرآیند انتگرال نیست. اگر شکل سطح مقطع عرضی نسبتاً استاندارد باشد، می‌توانید به سادگی معادله‌ای را که قبلاً برای سطح مقطع عرضی خاص شما استخراج شده است، جستجو کنید. اکثر کتاب‌های درسی مقاومت مصالح شامل جداول مشابه جدول زیر هستند که معادلات را برای مقاطع عرضی رایج فهرست می‌کنند.

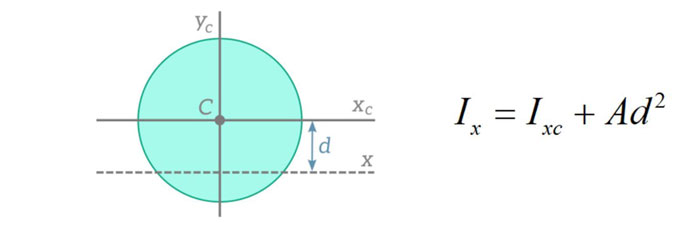
قضیه ی محور موازی

قضیه محورهای موازی یک تئوری فوق العاده مفید است که محاسبه ممان اینرسی سطح را برای محورهای خمش مختلف، بدون نیاز به مشتقگیری معادله از ابتدا با استفاده از روش انتگرال آسان میکند.

طبق این قضیه، ممان اینرسی سطح حول هر محور را می‌توان با استفاده از ممان اینرسی سطح حول یک محور موازی که از مرکز ثقل سطح مقطع می‌گذرد، مساحت مقطع و فاصله بین دو محور محاسبه کرد که دقیق تر این آموزش هارا به طور تخصصی میتوانید حتی در دوره آموزش سالیدورک نیز مشاهده نمایید

مرکز ثقل یک جسم صلب، نقطهای است که در آن وزن جسم به طور یکنواخت توزیع شده است. به عبارت دیگر، اگر جسم را روی یک سنجاق قرار دهید، جسم در حالت تعادل قرار خواهد گرفت. به مرکز ثقل جسم، گاهی اوقات نقطه تعادل نیز گفته میشود.

متون منابع مرجع به طور معمول معادلات ممان اینرسی سطح را برای محورهای مرکز ثقل ارائه میدهند. بنابراین قضیه محورهای موازی یک ابزار قدرتمند برای گسترش این معادلات به هر محور موازی دیگری است.

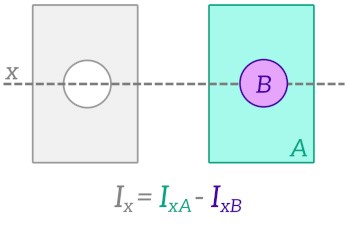
جمع و تفریق ممان اینرسی سطح

میتوان ممان اینرسی سطح را برای محاسبه مقادیر مقاطع مرکب جمع و تفریق کرد. تصویر زیر نشان میدهد که چگونه از این تکنیک میتوان برای محاسبه برای یک مقطع توخالی استفاده کرد.

هنگام استفاده از این روش، باید مطمئن شوید که مقادیر گشتاور دوم سطح برای مقاطع عرضی اجزا با محور خمش صحیح مطابقت دارند، در غیر این صورت ابتدا باید قضیه محورهای موازی را اعمال کنید تا مقادیر را برای محور خمشی صحیح به دست آورید.